Gaussian Function and its FT
Gaussian function is :
$f(x) = \dfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2}{2\sigma^2}}, x \in \mathbb{R}$
And a gaussian-like function holds the form of:
$f(x) = C_{1}e^{-C_{2}x^2}$ , where $C_{1}>0, C_{2}>0, C_{1}, C_{2} \in \mathbb{R} $
For the sake of conciseness, we consider the following form:
$f(x) = e^{-x^2}$
It has been an “obvious” conclusion taken for granted by many people that gaussian-like function’s fourier transformation is still gaussian-like. Almost all the computations I saw on Internet are as follows:
$F(w) = \int_{-\infty}^{\infty}f(x)e^{-iwx}dx$
$ = \int_{-\infty}^{\infty}e^{-(x^2+iwx)}dx$ ( using $ x^2 + iwx = (x + \frac{iw}{2})^2 - \frac{w^2}{4}$)
$= e^{-\frac{w^2}{4}}\int_{-\infty}^{\infty}e^{-(x + \frac{iw}{2})^2}dx$ ( substituting $x$ with $u=x+\frac{iw}{2}$ )
$= e^{-\frac{w^2}{4}}\int_{-\infty}^{\infty}e^{-u^2}du$
$= \sqrt{\pi}e^{-\frac{w^2}{4}}$
Done.
Delving into the computation
Anything wierd about the computation? In fact, it is only a “lucky computation” because the meaning of $\infty$ is totally misunderstood, even though the final result is right in value.
Here is the reason. In the above the integral with variable $x$, the integral region is from $-\infty$ to $\infty$ ,confined in real number field $\mathbb{R}$. The meaning is clear. However, in the integral with variable $u$ which is a complex variable with non-zero imaginary part, what does $\infty$ mean? For a complex variable with non-zero imaginary part, $\infty$ is meaningless because it is a concept of $\mathbb{R}$ ! Hence the $u$ based integral expression is invalid and meaningless ! If we have to substitute $u$ with $x$, the $u$ integral region should look like $-\infty + \frac{iw}{2}$ to $\infty + \frac{iw}{2}$. In summary, the substitution procedure is wrongly applied.
Nevertheless, $F(w) = \sqrt{\pi}e^{-\frac{w^2}{4}}$ is indeed correct. Why ?
The lucky point is that the following relation
$\int_{-\infty}^{\infty}e^{-(x + \frac{iw}{2})^2}dx = \int_{-\infty}^{\infty}e^{-x^2}dx$ (Eq. 1)
is correct, where $x$ is a real number variable. That is, if the forementioned $u$ is a completely new real number variable instead of a substitution of $x$ , the computation is correct.
This is why I call it a lucky computation because it is correct in shape but inaccurate in spirit. For an accurate computation of $F(w)$, we need to reasonably prove (Eq.1), and the mathematical knowledge required is complex integeral, rather than a trivial substitution.
Now let’s do it. I assume that readers have the basics of complex integral.
A complex integral is often a path integral. If the complex variable is denoted by $z$, integral in real number field actually corresponds to the path integral along the $Re(z)$ axis ( also called $x$ axis ) in the complex plane.
In this situation we need to apply the very classical and beautiful theorem in complex integral, Cauchy’s integral theorem:
$\oint_L{f(z)dz} = 0, z \in \mathbb{C}$
, if $f(z)$ is holomorphic in some region $U$ in the complex plane, and the integral is computed along a closed curve in $U$. ( for detailed statement, refer to Wiki. )
Apparently, function $f(z) = e^{-z^2}$ is holomorphic anythere in the whole complex plane, thus:
$\oint{e^{-z^2}dz} = 0$ (Eq.2)
holds along any closed curve in the complex plane. We choose to compute (Eq.2) along the following rectangular closed curve:
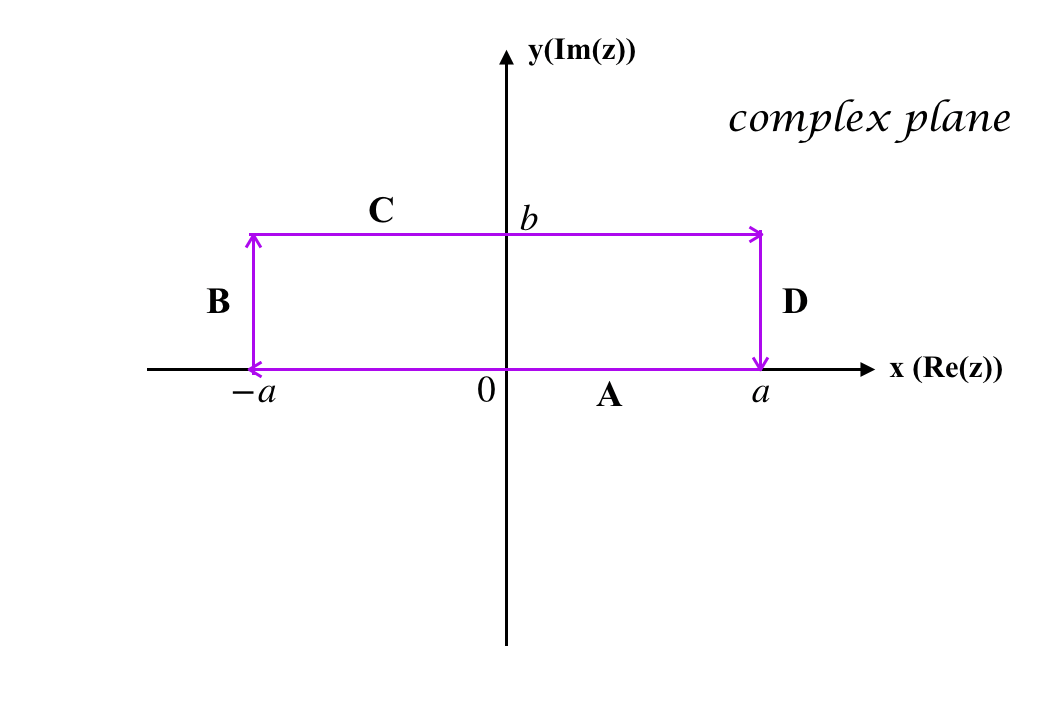
As drawn, the four edges of the rectangle are $A$, $B$, $C$, $D$. The “height” and “width” of the rectangle is $b$ and $2a$, where both $b$ and $a$ are real numbers. Thus expression (Eq.2) can be devided into four parts:
$\oint{e^{-z^2}dz} = \int_{A}{e^{-z^2}dz} + \int_{B}{e^{-z^2}dz} + \int_{C}{e^{-z^2}dz} + \int_{D}{e^{-z^2}dz} = 0$
Furthure, by separting $z$ into the form of $x+iy$ and $ x, y \in \mathbb{R}$, we have:
$\int_{A}{e^{-z^2}dz} = \int_{a}^{-a}{e^{-z^2}dz} = \int_{a}^{-a}{e^{-x^2}dx}$
$\int_{B}{e^{-z^2}dz} = \int_{-a}^{-a+ib}{e^{-z^2}dz} = \int_{0}^{b}{e^{-(-a+iy)^2}dy} = e^{-a^2}\int_{0}^{b}{e^{y^2+i2ay}}dy$
$\int_{C}{e^{-z^2}dz} = \int_{-a+ib}^{a+ib}{e^{-z^2}dz} = \int_{-a}^{a}{e^{-(x+ib)^2}dx}$
$\int_{D}{e^{-z^2}dz} = \int_{a+ib}^{a}{e^{-z^2}dz} = \int_{b}^{0}{e^{-(a+iy)^2}dy} = e^{-a^2}\int_{b}^{0}{e^{y^2-i2ay}}dy$
Next we do the limitation calculation. When $a$ goes to $\infty$ , it can be easily deduced that $\int_{B}$ and $\int_{D}$ goes to zero ( as an exercise if you are interested).
Therefore, we have:
$\lim_{a \to \infty} (\int_{a}^{-a}{e^{-x^2}dx} + \int_{-a}^{a}{e^{-(x+ib)^2}dx} ) = 0$
, which is :
$\int_{-\infty}^{\infty}{e^{-(x+ib)^2}dx} = \int_{-\infty}^{\infty}{e^{-x^2}dx}$
. (Eq.1) is proved.
Truely Done.
( still inaccurate ? Email me. )